Abstract: This paper introduces the concept of generalized reliability, and proposes the two-diameter path and the specific operational procedures for generalized reliability growth in the development of numerical control systems.
CNC systems are widely used in various types of electromechanical equipment. Due to the complexity of the CNC system and the importance of control, in general, its reliability requirements are high. High reliability is the guarantee for the application of advanced control methods. However, the reliability of any product has increased to a certain extent, and it is very difficult to raise it. Although it costs a lot of money, it has little effect. Because at this level, the defects that can be eliminated have been eliminated, leaving only defects that cannot be controlled or predicted. The fault caused by these defects is an accidental fault. It is difficult to eliminate.
For most CNC systems, although higher reliability is required, it is not completely unacceptable, so it is a repairable system. Since it is a repairable system. It is of little practical significance to talk about the narrow reliability of the system, but to consider the generalized reliability of maintenance.
1 The concept of generalized reliability
Generalized reliability is also called validity. For repairable products, it combines reliability and maintainability to evaluate products. Generalized reliability is a measure of generalized reliability and is the product in the specified alignment. The probability of being able to maintain work ability. Expressed by A(t), it is a function of time. For example, A(300)=0.96, which means that within 100 hours of 100 working hours, an average of 96 devices can be operated under normal conditions. As for the failure of several units during this period, it does not matter when it fails. As long as it is repaired within the specified time, it is guaranteed that 96 units will be met when the time is up to 300 hours. If a device A=0 96, it means that the device is 96% active, allowing faulty parking repair in the middle. This is different from R(300)=0 96, and R(300)=0 96 means that the probability of a device operating normally for 300 hours without failure is 96%. Generalized reliability is usually expressed by the instantaneous effective degree A(1), the average effective degree (T), and the time validity A.
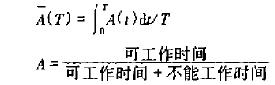
For accidents that occur in accidental faulty products, the change is not always called. The distribution of faultless operation is generally described by an exponential distribution, that is, the failure rate λ is constant. Similarly, the repair time of the product is also often described by an exponential distribution, ie the repair rate μ is constant. In most cases, the inoperable time is the repair time. and so
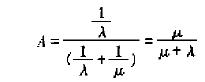
It can be seen from this equation that decreasing λ or increasing μ can increase the value of A. Therefore, the increase in the generalized reliability of the repairable system can be achieved by improving reliability or by improving maintainability.
2 The growth of generalized reliability of numerical control systems
The generalized reliability growth of numerical control systems must take into account the growth of reliability and maintainability. Of course, the growth of reliability still has to be given priority. Only when the cost for reliability growth exceeds the maintenance costs and downtime losses saved by reliability growth, and users do not have special requirements, do not continue to pursue reliability growth. The next focus of work should be shifted to improving maintainability.
In the development of numerical control systems, it is of course the best to reduce the cost or even improve the reliability or maintainability without spending money. There are also measures that can improve reliability and maintainability at the same time.
Next page
Heilongjiang Junhe Building Materials Technology Co., Ltd , https://www.junhejiancai.com