1 Spring-loaded mechanisms are often used in some measurement control instruments. For example, a spring force measuring mechanism is a mechanism with a spring. When the measured value changes, the position of the mechanism changes correspondingly due to the use of the elastic member, thereby indicating the magnitude of the measured value. However, the frame of such a device is often affected by vibration. Even if various anti-vibration measures are taken, the vibration of the frame will always be transmitted to the meter, which will affect the accuracy of the meter. In addition, the measured value itself is not static, and its fluctuations also affect the indication accuracy of the measuring instrument. The literature gives the series solution of the non-resonant condition of the Damper spring force measuring mechanism under the simple harmonic excitation. According to the different positions of the spring force measuring mechanism under the simple harmonic excitation, the analytical solution of the corresponding forced vibration is given. The literature considers the nonlinear factors of the spring force measuring mechanism, and analyzes the main resonance and singularity problems of the spring force measuring mechanism under the simple harmonic excitation. The following is a discussion of the force measuring mechanism shown in Fig. 1 to study the main parameter resonance problem which accounts for the influence of linear and nonlinear factors.
2 The position of the motion differential equation OA of the spring force measuring mechanism is represented by α. When the force F on the slider will be at a corresponding position, the force F balances the spring force (spring stiffness k) of the torsion spring acting on the rod OA. If the force F is a periodic disturbance force, for example, F will also vibrate. The rod OA will vibrate around an average position. This average position is called the dynamic equilibrium position and is represented by α. If it coincides with the static equilibrium position (indicated by a), the pointer will be error free. However, due to the influence of nonlinearity, α and α are different, which will bring the dynamic error of the indication. 0. The Lagrangian equation is used to establish the differential equation of motion of the graphic system, and the nonlinear vibration method is used to analyze the dynamic error Yang Zhian. Male, born in November 1963, Qinhuangdao, Hebei, Han nationality. He received his Ph.D. degree in general mechanics from Tianjin University in 1997. He is currently a professor at Tangshan College and a postdoctoral fellow at the School of Mechanical Engineering of Tianjin University. He is mainly engaged in the teaching and research of electromechanical coupling nonlinear dynamics and structure and vibration engineering.
Taking the generalized coordinate as ε, which is the swing angle of the rod OA from the dynamic equilibrium position α, it is considered that the clockwise direction is positive. Such a system of kinetic energy system's potential energy system dissipation function where μ is the damping coefficient and V is the initial value of the potential energy of the pointer in the vertical position.
The generalized force is the approximate value of F into the Lagrangian equation. After the finishing, the upper formula becomes the first approximate solution and the steady solution of the 3 main parameter resonance. 3.1 Theoretical analysis results due to damping term, nonlinear term and inertial force The term is a small term compared with the linear term. Therefore, the damping parameter and the nonlinear term are preceded by a small parameter γ. Because the main parameter resonance of the system needs to be studied, the constant term and the forced excitation term are ignored, and the equation (12) becomes Yang Zhi'an: The main parameter resonance study of the simple harmonic excitation spring force measuring mechanism is to substitute equations (14) and (15) into equation (12), and in order to simplify the research process, without loss of generality, in the case of main parameter resonance, Let ω'=1 γσ, where σ is the tuning value, using the multi-scale method [5~7], taking two time scales T1, and setting the first approximate solution in the case of the main parameter resonance to substituting equation (17) into 16), and using the derivative operator to represent, compare the coefficients of γ with the same power to obtain a set of partial differential equations. The solution of equation (18) is where cc represents the conjugate complex part of the right-end function of the equation.
The condition that the formula (20) is substituted into the right end of the formula (19) to eliminate the permanent term is to substitute the formula (21) into the formula (23), and the first approximation solution corresponding to the separation of the real part and the imaginary part is determined to determine the resonance of the corresponding main parameter. The constant solution, let β = 0 in equation (24), obtain the square of the algebraic equations and add them to obtain the amplitude α and phase β algebraic equation or the analytical equation (28). When different solutions are obtained, there are 0 In time, there are c) in other regions only a 3.2 numerical analysis result (28) is the main parameter common amplitude frequency response equation, and the response curve of the main parameter resonance can be calculated by using equation (28), and the response curves of different parameters are analyzed. Impact. If there is no special declaration parameter value, m = can be seen from Figures 2 and 3, the force amplitude response curve is the same whether the hard stiffness system or the soft stiffness system is the same. Figure 4, the rigid stiffness system or the soft stiffness system, as the damping of the mechanism increases, the dynamic error of the pointer, that is, the swing angle of the rod OA from the dynamic equilibrium position α is decreasing. At the same time, the resonance range of the pointer is also reduced.
1) Establish a nonlinear vibration equation with a damped spring force measuring mechanism subjected to harmonic excitation.
2) Obtain a first approximate solution of the main parameter resonance of the nonlinear vibration equation.
3) Under the same parameters, the force amplitude and frequency response curves of the hard stiffness system and the soft stiffness system are the same.
4) As the damping decreases and the harmonic excitation amplitude increases, the peak and resonance regions of the system amplitude response curve increase.
5) Under the same parameters, the force amplitude frequency response curve of the hard stiffness system and the soft stiffness system is about σ antisymmetry.
The above conclusions are theoretical analysis and numerical calculation results.
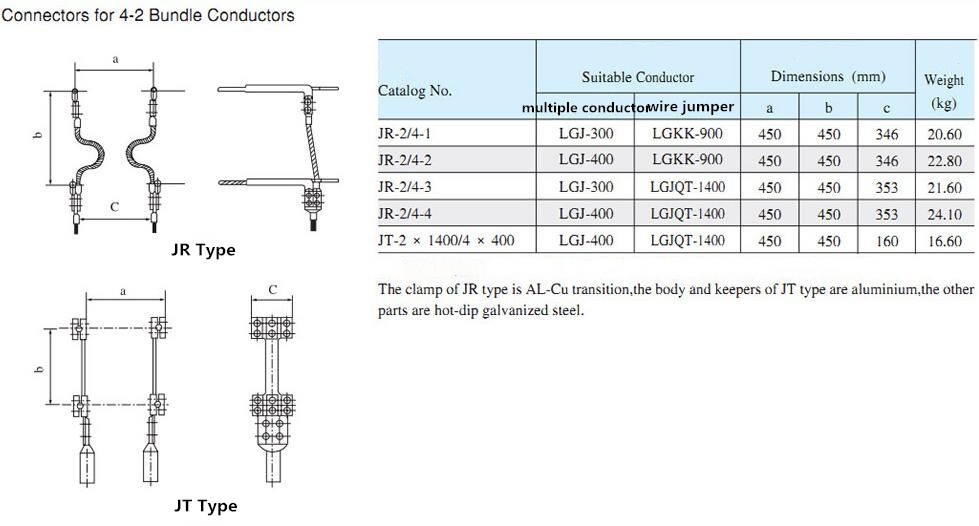
Our connector for 4-2 bundle conductors----JTL-2/4-300/40-900K, four leads and another two leads could be ordered according to the customers practical demand, the consumer should give clear indication of the lead kind. Splicing fittings are used for splicing or repairing conductor and ground wire of overhead transmission lines. The splices may be compression type, bolt type performed armour rods in accordance with the construction and mounting way. The compressive splices have hydraulic, explosive and notched type. The DC resistance of all splices must be less thank that of the equi-length conductor, the temperature rise of all aplices must be less thank that of the aplicing conductor. The slip strength of the compressive sleeve must be not less than 95% of the rated strength of conductor.


If you have any questions, please contact with us directly.
Our company is solemnly committed to the majority of customers: reasonable price, short production cycle, considerate service. We look forward to cooperating with you.
Connector For 4-2 Bundle Conductor
Connector For 4-2 Bundle Conductor,4-2 Bundle Conductor Connector,Connectors For 4-2 Bundle Conductor,Connectors For Bundle Conductors
Shandong Vantage International Trade Co., Ltd. , https://www.steelplate.be